Question

If A( 1,8) B(2,6) and C(4,2) are three points, show that AC=3AB​

Answer 1

see explanation

Explanation:

Calculate AC and AB using the distance formula

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

with (x₁, y₁ ) = A(1,8) and (x₂, y₂ ) = C(4,2)

AC =
`√((4-1)^2+(2-8)^2)`

=
`√(3^2+(-6)^2)`

=
`√(9+36)`

=
`√(45)` =
`√(9(5))` = 3
`√(5)`

Repeat with

(x₁, y₁ ) = A(1, 8) and (x₂, y₂ ) = B(2, 6)

AB =
`√((2-1)^2+(6-8)^2)`

=
`√(1^2+(-2)^2)`

=
`√(1+4)`

=
`√(5)`

So AB =
`√(5)` and AC = 3
`√(5)`

Thus

AC = 3AB

Answer 2

Proven below

Explanation:

Distance Between Points in the Plane

Given two points A(x,y) and B(w,z), the distance between them is:

`d=√((w-x)^2+(z-y)^2)`

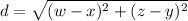
Let's calculate the distance AC, where A(1,8) and C(4,2):

`d_(AC)=√((4-1)^2+(2-8)^2)`

`d_(AC)=√(3^2+(-6)^2)`

`d_(AC)=√(9+36)=√(45)`

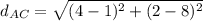
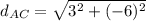
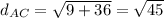
Since 45=9*5:

`d_(AC)=√(9*5)=3√(5)`

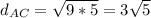
Calculate the distance AB, where A(1,8) and B(2,6)

`d_(AB)=√((2-1)^2+(6-8)^2)`

`d_(AB)=√(1^2+(-2)^2)`

`d_(AB)=√(1+4)=√(5)`

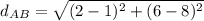
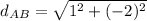
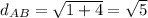
It follows that:

`d_(AC)=3d_(AB)`