Question

How does one find the inverse function of f(x)=
`(1)/(3x-1)`

Answer 1

`\displaystyle f^(-1)(x)=(1+x)/(3x)`

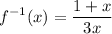
Explanation:

The Inverse of a Function

The procedure to find the inverse of the function is:

* Write the function as a two-variable equation:

`\displaystyle y=(1)/(3x-1)`

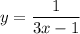
* Solve the equation for x.

Multiply by 3x-1

`y(3x-1)=1`

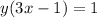
Divide by y:

`\displaystyle 3x-1=(1)/(y)`

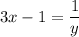
Sum 1:

`\displaystyle 3x=(1)/(y)+1`

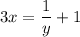
Operate the right side:

`\displaystyle 3x=(1+y)/(y)`

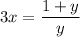
Divide by 3:

`\displaystyle x=(1+y)/(3y)`

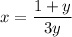
* Swap the variables:

`\displaystyle y=(1+x)/(3x)`

Write back into function form:

`\boxed{\displaystyle f^(-1)(x)=(1+x)/(3x)}`