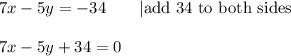Answer:
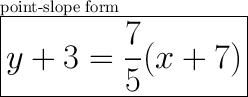

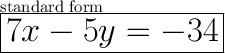
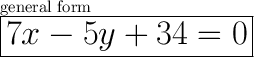
Explanation:
The slope-point form of an equation of a line:

where
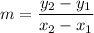
From the graph we have two points (-7, -3) and (-2, 4).
Substitute:
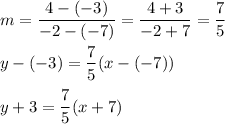
Convert to the slope-intercept form (y = mx + b):

Convert to the standard form (Ax + By = C):

Convert to the general form (Ax + By + C = 0):