Answer:
The largest n for which
 is a divison of 80 is 4.
is a divison of 80 is 4.
Explanation:
Numbers can be composited, that is, a product of prime numbers, or primer numbers themselves. A entire number is a divisor of another entire number if result is an entire number.
As first step we need to decompose 80 as a product of prime numbers, whose procedure is presented below:
1)
 Given
Given
2)
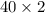 Definition of multiplication.
Definition of multiplication.
3)
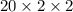 Definition of multiplication.
Definition of multiplication.
4)
 Definition of multiplication.
Definition of multiplication.
5)
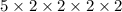 Definition of multiplication.
Definition of multiplication.
6)
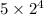 Definition of power/Result.
Definition of power/Result.
In a nutshell, the largest n for which
 is a divison of 80 is 4.
is a divison of 80 is 4.