Answer:

Explanation:
We have the equation:
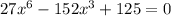
We can solve this using u-substitution. Let's let u=x³. Therefore:
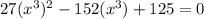
Substitute all x³s for u:

This is now in quadratic form. So, we can use the quadratic formula:
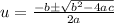
Our a is 27, b is -152, and c is 125. So:
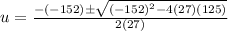
Simplify:

Simplify:
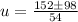
Reduce. Divide everything by 2:

Split into two cases:
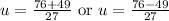
Solve for each case:

Substitute back x³ for our u:
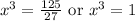
Take the cube root of each equation:
![x=\sqrt[3]{(125)/(27)}\text{ or } x=\sqrt[3]1](https://img.qammunity.org/2021/formulas/mathematics/high-school/mbqg9jygjnd8vr7kblsr8cxqkn9gf40035.png)
Evaluate:

And that's our two solutions.
And we're done!