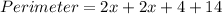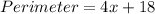Question

Suppose a rectangular garden plot has a length that can be expressed as x+2 feet and a width expressed as x+7 feet. Write a polynomial expression to represent the area of the garden? Write a polynomial expression to represent the perimeter of the garden?

Answer 1

`Area = x^2 + 9x + 14`

`Perimeter = 4x + 18`

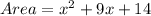
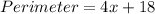
Explanation:

Given:

Length of rectangular garden = (x + 2) ft

Width = (x + 7) ft

Required:

a. Polynomial expression of the area of the garden

b. Polynomial expression of the perimeter of the garden

SOLUTION:

Area of the rectangular garden = length × width

`Area = (x + 2)(x + 7)`

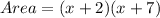
Expand using the distributive property of multiplication

`Area = x(x + 7) +2(x + 7)`

`Area = x^2 + 7x + 2x + 14`

`Area = x^2 + 9x + 14`

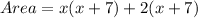
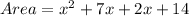
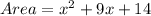
Perimeter = 2(length) + 2(width)

`Perimeter = 2(x + 2) + 2(x + 7)`

`Perimeter = 2x + 4 + 2x + 14`

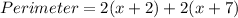
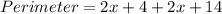
Collect like terms

`Perimeter = 2x + 2x + 4 + 14`

`Perimeter = 4x + 18`