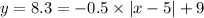Question

the side elevation of a storage building is mapped on a coordinate grid. which equation could be used to determine the corresponding x value(s) of the roof line when y=8.3?​

Answer 1

The correct option is;

`8.3 = -0.5 * \left | x -5 \right | + 9`

Explanation:

The coordinates of the roof are;

Starting point, = (1, 7)

Maximum height = (5, 9)

Maximum range = (9, 7)

The slope of the left portion of the roof = (9 - 7)/(5 - 1) = 0.5

The equation of the left portion of the roof is given as follows;

y - 9 = 0.5 × (x - 5)

y = 0.5 × (x - 5) + 9

The slope of the right portion of the roof = (7 - 9)/(9 - 5) = -0.5

The equation of the right portion of the roof is given as follows;

y - 9 = -0.5 × (x - 5)

y = -0.5 × (x - 5) + 9

However, when x < 5, we have;

`0.5 * \left | x -5 \right |= -0.5 * \left | x -5 \right |`

`\therefore y = 0.5 * \left | x -5 \right | + 9 = -0.5 * \left | x -5 \right | + 9 = 0.5 * \left ( x -5 \right ) + 9`

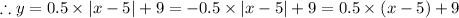
When x > 5, we have;

`0.5 * \left | x -5 \right |> -0.5 * \left | x -5 \right |`

`\therefore y = -0.5 * \left | x -5 \right | + 9 = -0.5 * \left ( x -5 \right ) + 9`

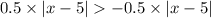
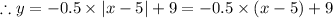
Therefore, the equation that applies to both the left and right portion of the roof is
`y = -0.5 * \left | x -5 \right | + 9`

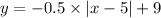
Which gives the correct option as follows;

`y = 8.3 = -0.5 * \left | x -5 \right | + 9`