Answer:
(x-8)² + (y-5)² = 400
Explanation:
general equation of a circle : (x-h)² + (y-k)² = r²
where (h,k) is at center and r = radius
here we are given the center as well as a point on the circle
first we will need to identify the radius by finding the distance between the center and the point on the circle using using the distance formula ( we know this is the radius because the radius is a line that goes on the center of the circle to any point on the circle )
Identifying the radius using the distance formula
Distance formula :
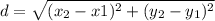
where the x and y values are derived from the two given points
Given points are (8,5) and (-4,21)
Assigning variables we get (x1,y1) = (8,5) , so x1 = 8 and y1 = 5
and (x2,y2) = (-4,21) so x2 = -4 and y2 = 21
Plugging this into the formula we get
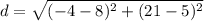
==> subtract values inside of parenthesis
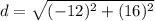
==> evaluate exponents
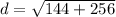
==> add 144 and 256
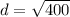
==> take the square root of 400
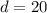
so the radius is 400
Finding the equation of the circle
again we have the general equation of a circle as (x-h)² + (y-k)² = r²
where (h,k) is at center and r = radius
here the center is at (8,5) and the radius is 20
so (h,k) = (8,5) so h = 8 and k = 5 and radius is 20 so r = 20
plugging these values into the general equation of a circle we get
(x-8)² + (y-5)² = 20²
==> evaluate exponent
(x-8)² + (y-5)² = 400
and we are done!
For more validation check the attached image :)