Question

Please help the distance formula

Answer 1

7.8

Explanation:

distance formula :
`d = √((x_2-x_1)^2+(y_2-y_1)^2)`

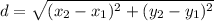
where the x and y values are derived from the given points

here the given points are (11,3) and (6,9)

assigning variables

(x1,y1) = (11,3) so x1 = 11 and y1 = 3

(x2,y2) = (6,9) so x2 = 6 and y2 = 9

plugging in values into formula

recall formula
`d = √((x_2-x_1)^2+(y_2-y_1)^2)`

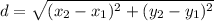
==> plug in x1 = 11 , y1 = 3 , x2 = 6 and y2 = 9

`d=√((6-11)^2+(9-3)^2)`

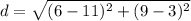
==> subtract values in parenthesis

`d=√((-5)^2+(6)^2)`

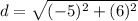
==> evaluate exponents

`d=√(25+36)`

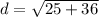
==> add 25 and 36

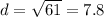`d=√(61)=7.8` ( approximately )