Hey ! there
Answer:
Explanation:
In this question we are provided with right angle triangle having hypotenuse ( longest side ) = c , perpendicular = 5 and base = 12 . And we are asked to find the length of missing side i.e. hypotenuse and if necessary we have to round it off to 2 decimal places.
We can find the missing side by using Pythagorean Theorem . It states that sum of squares of perpendicular and base is equal to square in a right angle triangle that is ,
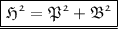
Where ,
- P refers to Perpendicular
SOLUTION : -
Substituting value of hypotenuse as c , perpendicular as 5 and base as 12 in formula :
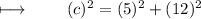
Squaring 5 and 12 :
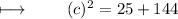
Adding 25 and 144 :
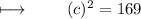
Applying square root to both sides :
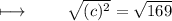
On simplifying , We get :

- Henceforth , ❝ 13 ❞ is the length of missing side .
Verifying : -
Now we are checking our answer by putting all values in formula . So ,
- ( 13 )² = ( 5 )² + ( 12 )²
Therefore , our answer is correct .
#Keep Learning