Answer:
C. 26 yards
Explanation:
Jamie's fence total length = perimeter of the polygon
Perimeter of the polygon = AB + BC + CD + DE + EF + FA
AB, FA and DE can be worked accordingly as shown below:
AB = |-5 - 0| = 5 units
FA = |5 - 2| = 3 units
DE = |1 -(-2)| = 3 units
BC, CD, and EF can be calculated using the formula
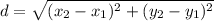
Distance between B(0, 5) and C(4, 2):
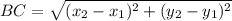
Let,
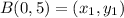
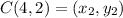
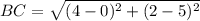
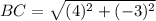
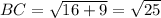
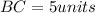
Distance between C(4, 2) and D(1, -2)
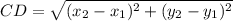
Let,
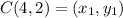
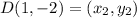
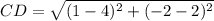
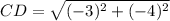
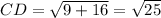
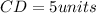
Distance between E(-2, -2) and F(-5, 2):
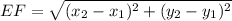
Let,
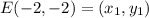
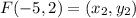
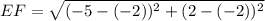
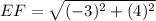
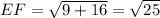
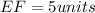
Total length of the wall in yards = 5 + 5 + 5 + 3 + 5 + 3 = 26 yards