Answer:

Explanation:
Let's look at this triangle.
━━━━━━━━━▼━━━━━━━━━
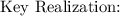
we can see that the line intersecting the triangle has cut our triangle into two parts. Since this line is parallel to the bottom of the triangle, ∠2 and ∠1 are corresponding angles, meaning their measurements are the same.
━━━━━━━━━▲━━━━━━━━━
Since we know the measure of both, we can set both equal to each other.
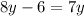
Now we solve for y.
Subtract 8y from both sides:
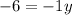
Divide both sides by -1:
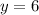
Great! Now that we know y, we can substitute it into the equation for ∠2,
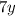
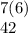
Hope this helped!