Given:
Endpoints of segment AB are A(- 18, 5) and B(- 4, 5).
Point Z is located exactly 1/8 of the distance from A to B.
To find:
The value of the x-coordinate of point Z.
Solution:
Point Z is located exactly 1/8 of the distance from A to B.
AZ:AB=1:8
AZ:ZB = AZ:(AB-AZ)= 1:(8-1) = 1:7
It means point Z divided segment AB in 1:7.
Using section formula, the x coordinate of point Z is
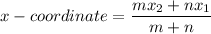
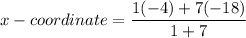
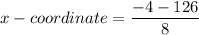
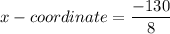
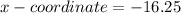
Therefore, the required x-coordinate of point Z is -16.25.