Question

The average yearly snowfall in Chillyville is Normally distributed with a mean of 55 inches. If the snowfall

in Chillyville exceeds 60 inches in 15% of the years, what is the standard deviation?
a) 4.83 inches
b) 8.93 inches
c) 5.18 inches
d) 6.04 inches
e) The standard deviation cannot be computed from the given information.

Answer 1

The standard deviation is 4.83 inches.

Step-by-step explanation:

We are given that the average yearly snowfall in Chillyville is Normally distributed with a mean of 55 inches.

The snowfall in Chillyville exceeds 60 inches in 15% of the years, we have to find the standard deviation.

Let X = the average yearly snowfall in Chillyville.

The z-score probability distribution for the normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean amount of rainfall = 55 inches

`\sigma` = standard deviation

Now, it is stated that the snowfall in Chillyville exceeds 60 inches in 15% of the years, that means;

P(X > 60 inches) = 0.15

P(
`(X-\mu)/(\sigma)` >
`(60-55)/(\sigma)` ) = 0.15

P(Z >
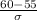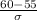`(60-55)/(\sigma)` ) = 0.15

In the z table, the critical value of z that represents the top 15% of the area is given as 1.0364, that means;

`(60-55)/(\sigma) = 1.0364`

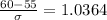
`\sigma} = (5)/(1.0364)` = 4.83 inches

Hence, the standard deviation is 4.83 inches.