Question

An Olympic-class sprinter starts a race with an acceleration of

4.50 m/s^2
. (a) What is her speed 2.40 s later? (b) Sketch a graph of her position vs. time for this period.

Answer 1

a) Vf = 10.8 [m/s]

b) See the image attached.

Step-by-step explanation:

a)

To solve this part we must use the following kinematics equation:

`v_(f) =v_(o) + (a*t)`

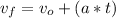
where:

Vf = final velocity [m/s^2]

Vo = initial velocity = 0

a = aceleration = 4.5 [m/s^2]

t = time = 2.4 [s]

Note: The initial velocity is taken as zero, as the athlete starts from rest

Vf = 0 + (4.5*2.4)

Vf = 10.8 [m/s]

b)

Now knowing that acceleration remains constant between the time interval between 0 to 2.4 seconds. We will take 5 different times between the 2.4 elapsed.

Dt = 2.4/5

Dt = 0.48 [s]

So the first time is 0, the second will be (0 + 0.48) = 0.48, the third (0.48 + 0.48) = 0.96, the fourth (0.96 + 0.48) = 1.44, and the fifth (1.44 + 0,48) = 1.92, and the last one (1.92 + 0.48) = 2.4

We need to find the velocity for each time calculated before, with the ecuation used in a) we cand calculate the different velocities.

Vfo = 0 + (4.5*0) = 0

Vf1 = 0 + (4.5*0.48) = 2.16 [m/s]

Vf2 = 0 + (4.5*0.96) = 4.32 [m/s]

Vf3 = 0 + (4.5*1.44) = 6.48 [m/s]

Vf4 = 0 + (4.5*1.92) = 8.64 [m/s]

Vf5 = 0 + (4.5*2.4) = 10.8 [m/s]

The next step is to use the following equation of kinematics, to be able to determine the position of the athlete for each speed.

`v_(f)^(2) =v_(i)^(2) +(2*a*x)\\if \\v_(i)=0\\then\\x = (v_(f)^(2))/(2*a)`

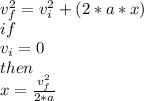
x1 = 0

x2 = (2.16)^2/(2*4.5) = 0.518 [m]

x3 = (4.32)^2/(2*4.5) = 2.074 [m]

x4 = (6.48)^2/(2*4.5) = 4.67 [m]

x5 = (8.64)^2/(2*4.5) = 8.29 [m]

x6 = (10.8)^2/(2*4.5) = 12.96 [m]

Now in the x-axis we put the time values found before as well the x values en the y-axis.