Question

30. Find the smallest positive integer j for which the statement is true. Use the extended principle of mathematical induction to prove that the formula is true for every integer greater than j .

n^{2} \leq 2^{n}

Answer 1

n² ≤ 2ⁿ , ∀ n ≥ 4

Explanation:

`4^(2)=16 \leq16=2^(4)`

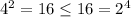
Then ,For n = 4 the inequality is true.

For n ≥ 4 , suppose n² ≤ 2ⁿ and prove that (n+1)² ≤ 2ⁿ⁺¹

(n+1)² = n² + 2n + 1

Since n² ≤ 2ⁿ (according to the hypothesis) and we know that 2n + 1 ≤ 2ⁿ

Then

(n+1)² = n² + 2n + 1 ≤ 2ⁿ + 2ⁿ

Then

(n+1)² ≤ 2ⁿ + 2ⁿ

Then

(n+1)² ≤ 2×2ⁿ

Then

(n+1)² ≤ 2ⁿ⁺¹

Conclusion:

n² ≤ 2ⁿ , ∀ n ≥ 4