Question

`\begin{aligned} &\text { 55. At which term does the sequence }\\ &\{10,12,14.4,17.28, \ldots\} \text { exceed } 100 ? \end{aligned}`

Answer 1

14th term

Explanation:

12÷10 = 1.2

14.4÷12 = 1.2

17.28÷14.4 = 1.2

Then it’s a geometric sequence of first term ‘V₀=10’ and common ration ‘q = 1.2’

We call it (Vn)

The general term of the sequence:

Vn = V₀×qⁿ⁻¹ = 10×(1.2)ⁿ⁻¹

To determine the term at which the sequence exceeds 100 we have to solve the equation:

Vn ≥ 100

⇔ 10×(1.2)ⁿ⁻¹ ≥ 100

⇔ (1.2)ⁿ⁻¹ ≥ 100/10

⇔ (1.2)ⁿ⁻¹ ≥ 10

⇔ ln(1.2)ⁿ⁻¹ ≥ ln(10)

⇔ (n-1)×ln(1.2) ≥ ln(10)

`\Longleftrightarrow n-1\geq(ln10)/(ln1.2)`

`\Longleftrightarrow n-1\geq12.6\\\Longleftrightarrow n\geq13.6\\\Longrightarrow n=14`

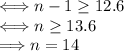
Verification:

`V_(14)=10* \left( 1.2\right)^(14-1) =106.993205379072`