Question

The dipole moment of water is p = 6.17 x 10-30 C m. If the electric field in a microwave oven is on average 94.7 x 10-6 N/C, and water molecules start anti-parallel to the external field (180o), how much energy (in Joules) is deposited into a water sample in 2.39 seconds with 13.1 of water if the direction of this field switches every 3.42 x 108 times a second and each time the electric field flips the water molecules align themselves with the new direction?

Answer 1

Step-by-step explanation:

Given that:

p = 6.17 × 10⁻³⁰ Cm

Electric field E = 94.7 × 10⁻⁶ N/C

Then:

`U= -p^(\to) *E^(\to)`

`U_i = -pE \ cos180^0 =pE \\ \\ U_f = -pE \ cos 0^0 = -pE`

∴

`\Delta U = U_i - U_f = 2pE \ \ per \ dilute/per \ switch`

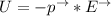
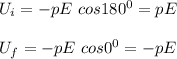
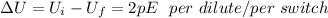
This implies that one switch of dipole produces 2pE energy to be deposited in the water.

mass of water = 13.1 g

The number of water molecule =
`(mass)/(molar \ mass)* N_A`

=
`(13.1)/(18.015)*6.023 * 10^(23)`

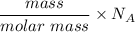
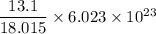
= 4.38 × 10²³ molecules of water.

∴ Number of dipoles = 4.38 × 10²³

The total number of switches in 2.39 sec = switch frequency × 2.73

Number of switches = 2.39 × 3.42 × 10⁸

Number of switches = 817380000

Number of switches = 8.174 × 10⁸

The total energy Q deposited = Energy deposited per dipole × Number of dipole × no of switches

Q = (2pE) × 4.38 × 10²³ × 8.174 × 10⁸

Q = (2 × 6.17 × 10⁻³⁰ × 94.7 × 10⁻⁶ × 4.38 × 10²³ × 8.174 × 10⁸ )

Q = 0.41838 J