Answer:
The minimum acceleration his partner will need in order to catch Bond before he hits the water is 25.688 meters per square second.
Step-by-step explanation:
Let be the initial position of the sppedboat the reference location, James Bond jumps horizontally and experiments a parabolic motion, which consists in a horizontal motion at constant velocity and an vertical uniform accelerated motion due to gravity.
Speedboat must accelerate from rest and get Bond at right location and instant. Now we describe the appropriate equations of motion for James Bond and for the speedboat:
James Bond
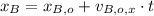
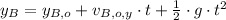
Speedboat
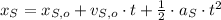
Where:
 ,
,
 - Initial horizontal positions for James Bond and the speedboat, measured in meters.
- Initial horizontal positions for James Bond and the speedboat, measured in meters.
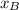 ,
,
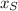 - Current horizontal positions for James Bond and the speedboat, measured in meters.
- Current horizontal positions for James Bond and the speedboat, measured in meters.
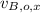 ,
,
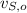 - Initial horizontal velocities of James Bond and the speedboat, measured in meters per second.
- Initial horizontal velocities of James Bond and the speedboat, measured in meters per second.
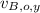 - Initial vertical velocity of James Bond, measured in meters per second.
- Initial vertical velocity of James Bond, measured in meters per second.
 - Time, measured in seconds.
- Time, measured in seconds.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 - Acceleration of the speedboat, measured in meters per square second.
- Acceleration of the speedboat, measured in meters per square second.
We must observe the following conditions such as we may calculate the minimum acceleration of the speedboat:
1)
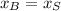
2)
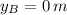
Now, if we know that
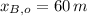 ,
,
 ,
,
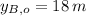 ,
,
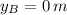 ,
,
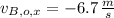 ,
,
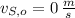 ,
,
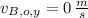 and
and
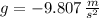 , the resulting system of equations is:
, the resulting system of equations is:
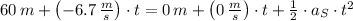
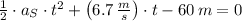 (Eq. 1)
(Eq. 1)
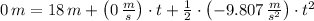
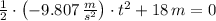 (Eq. 2)
(Eq. 2)
At first we get the time from (Eq. 2) by using the Quadratic Formula:
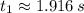 and
and
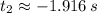
Only the first root is physically reasonable. (
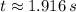 )
)
Then, we substitute time in (Eq. 1) and clear the acceleration of the speedboat:


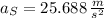
The minimum acceleration his partner will need in order to catch Bond before he hits the water is 25.688 meters per square second.