Question

2013 Indianapolis 500 champion Tony Kanaan holds his hand out of his IndyCar while driving through still air with standard atmospheric conditions. (a) For safety, the pit lane speed limit is 60 mph. At this speed, what is the maximum pressure on his hand? (b) Back on the race track, what is the maximum pressure when he is driving his IndyCar at 225 mph? (c) On the straightaways, the IndyCar reaches speeds in excess of 235 mph. For this speed, is your solution method for parts (a and (b) reasonable? Explain.

Answer 1

(a). The pressure is 14.76 psi.

(b). The pressure is 15.59 psi.

(c). The pressure is 15.68 psi.

All answer are reasonable.

Step-by-step explanation:

Given that,

Speed v₁= 60 mph

Speed v₂ = 225 mph

Speed v₃ = 235 mph

(a). We need to calculate the maximum pressure on his hand

Using equation of pressure

`P_(1)=P+(1)/(2)\rho v^2+\rho gh`

there, no vertical movement

So, on neglect of height term

`P_(1)=P+(1)/(2)\rho v_(1)^2`

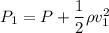
Where, P= atmospheric pressure

`\rho` = air density

v = speed

Put the value in the equation

`P_(1)=14.7*144+(1)/(2)*(0.002376*(60*1.4667)^2)`

`P_(1)=2126.0\ lb/ft^2`

`P_(1)=(2126.0)/(144)`

`P_(1)= 14.76\ psi`

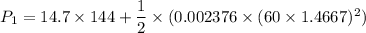
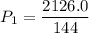
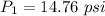
(b). Speed v₂ = 225 mph

We need to calculate the maximum pressure on his hand

Using equation of pressure

`P_(2)=P+(1)/(2)\rho v_(2)^2`

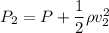
Put the value in the equation

`P_(2)=14.7*144+(1)/(2)*(0.002376*(225*1.4667)^2)`

`P_(2)=2246.17\ lb/ft^2`

`P_(2)=(2246.17)/(144)`

`P_(2)= 15.59\ psi`

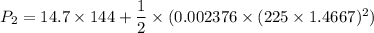
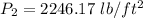
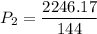
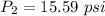
(c). Speed v₃ = 235 mph

We need to calculate the maximum pressure on his hand

Using equation of pressure

`P_(3)=P+(1)/(2)\rho v_(3)^2`

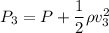
Put the value in the equation

`P_(3)=14.7*144+(1)/(2)*(0.002376*(235*1.4667)^2)`

`P_(3)=2257.93\ lb/ft^2`

`P_(3)=(2257.93)/(144)`

`P_(3)= 15.68\ psi`

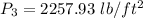
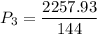
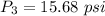
According to bernoulli's equation,

If the car increases the velocity the the pressure on the surface of the driver's hand increases.

The pressure from P₁ to P₃ are all near the value of one atmosphere.

So, the pressure difference of one atmosphere is not enough to break the driver's hand.

Hence, (a). The pressure is 14.76 psi.

(b). The pressure is 15.59 psi.

(c). The pressure is 15.68 psi.

All answer are reasonable.