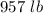Answer:
The quantity of salt is "957 lb". A further explanation is given below.
Step-by-step explanation:
(1)
As we know,
1 hour 40 Min
= 60 min + 40 min
= 100 min
Salt water is going in at the rate of 2 gal/min
Salt water went into the tank in 100 min will be:
=
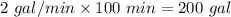
We have 1.92 lb of salt per gal.
In 200 gal, salt went in 1 hour 40 min will be:
=
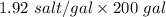
=
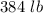
Now,
ft3 = 7.5 gal
The density of solution will be:
=
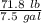
=
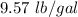
The solution went out in 100 min 1920 lb as well as going out at 19.2 lb per min.
=
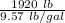
=
 (salt went out)
(salt went out)
The salt remained in the tank at the end of 1 hour 40 min i.e.,
=
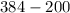
=
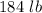
(2)
As well as the upper limit for the no. of pounds for continues stirring indefinitely per 100 gal will be:
=