Question

The Reviews editor for a certain scientific journal decides whether the review for any particular book should be short (1–2 pages), medium (3–4 pages), or long (5–6 pages). Data on recent reviews indicates that 50% of them are short, 30% are medium, and the other 20% are long. Reviews are submitted in either Word or LaTeX. For short reviews, 70% are in Word, whereas 50% of medium reviews are in Word and 30% of long reviews are in Word. Suppose a recent review is randomly selected.(a) What is the probability that the selected review was submitted in Word format?(b) If the selected review was submitted in Word format, what are the posterior probabilities of it being short, medium, or long? (Round your answers to three decimal places.)shortmediumlong

Answer 1

The probability that the selected review was submitted in Word format is 0.56.

Explanation:

We are given that Data on recent reviews indicates that 50% of them are short, 30% are medium, and the other 20% are long. Reviews are submitted in either Word or LaTeX. For short reviews, 70% are in Word, whereas 50% of medium reviews are in Word and 30% of long reviews are in Word.

Let the probability that there are short reviews = P(S) = 0.50

The probability that there are medium reviews = P(M) = 0.30

The probability that there are long reviews = P(L) = 0.20

Let W = event that the reviews are submitted in either Word or LaTeX

So, the probability that short reviews are submitted in Word = P(W/S) = 0.70

The probability that medium reviews are submitted in Word = P(W/M) = 0.50

The probability that long reviews are submitted in Word = P(W/L) = 0.30

(a) The probability that the selected review was submitted in Word format is given by = P(W)

P(W) = P(S)
`*` P(W/S) + P(M)
`*` P(W/M) + P(L)
`*` P(W/L)

= (0.50
`*` 0.70) + (0.30
`*` 0.50) + (0.20
`*` 0.30)

= 0.35 + 0.15 + 0.06

= 0.56

Hence, the probability that the selected review was submitted in Word format is 0.56.

(b) Now, if the selected review was submitted in Word format, the posterior probabilities of it being short is given by = P(S/W)

P(S/W) =
`(P(S) * P(W/S))/(P(S) * P(W/S)+P(M) * P(W/M)+P(L) * P(W/L))`

=
`(0.50* 0.70)/(0.50* 0.70+0.30* 0.50+0.20* 0.30)`

=
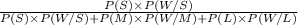
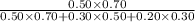
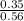`(0.35)/(0.56)` = 0.625

Similarly, if the selected review was submitted in Word format, the posterior probabilities of it being medium is given by = P(M/W)

P(M/W) =
`(P(M) * P(W/M))/(P(S) * P(W/S)+P(M) * P(W/M)+P(L) * P(W/L))`

=
`(0.30* 0.50)/(0.50* 0.70+0.30* 0.50+0.20* 0.30)`

=
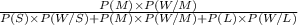
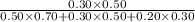
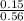`(0.15)/(0.56)` = 0.268

Also, if the selected review was submitted in Word format, the posterior probabilities of it being long is given by = P(L/W)

P(L/W) =
`(P(L) * P(W/L))/(P(S) * P(W/S)+P(M) * P(W/M)+P(L) * P(W/L))`

=
`(0.20* 0.30)/(0.50* 0.70+0.30* 0.50+0.20* 0.30)`

=
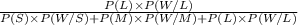
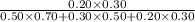
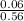`(0.06)/(0.56)` = 0.107.