Answer:
C. The arc lengths are proportional: Arc C D = 4 arc E F.
Explanation:
The question is incomplete. Here is the complete question.
In each circle below, a 50° angle with a vertex at the center of the circle is drawn. How are minor arc lengths CD and EF related?
Circle A and B are shown. Line segments D A and C A are radii with lengths of 8 centimeters. Angle D A C is 50 degrees. Line segments F B and E B are radii with lengths of 2 centimeters. Angle F B E is 50 degrees.
They are the same because the central angle measure is the same.
The arc lengths are proportional: Arc C D = 2 arc E F.
The arc lengths are proportional: Arc C D = 4 arc E F.
The arc lengths are proportional: Arc C D = 6 arc E F.
Using the formula for calculating the length of an arc to find the length of both arcs.
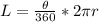
For the minor arc CD:
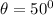
r = 8cm
L = 50/360 * 2π(8)
L = 5/36 * 16π
L = 80π/36
Length of CD = 20π/9 cm²
For the minor arc EF:
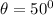
r = 2cm
L = 50/360 * 2π(2)
L = 5/36 * 4π
L = 20π/36
Length of arc EF = 5π/9 cm²
Find the relationship between both lengths:
From CD = 20π/9 cm²
CD = 4 * (5π/9 cm²)
since length of arc EF = 5π/9 cm²
Then arc CD = 4* arc EF
This shows that the length of arc CD is four times that of arc EF