Question

"D" size batteries produced by MNM Corporation have had a life expectancy of 87 hours. Because of an improved production process, it is believed that there has been an increase in the life expectancy of its "D" size batteries. A sample of 80 batteries showed an average life of 88.5 hours. Assume from past information that it is known that the standard deviation of the population is 9 hours. Conduct a hypothesis test to determine whether there is statistically significant evidence to support that the life expectancy of batteries have improved. What is the p-value associated with the sample results?

Answer 1

As p-value = 0.0.68 > 0.05 the null hypothesis could not be rejected

Explanation:

The computation of the p-value is shown below:

Given that

Average life =
`\bar x` = 88.5

Standard deviation =
`\sigma` = 9

Sample = n = 80

Based on the above information

Null and alternative hypothesis is

`H_o : u = 87\\\\H_a : u > 87`

Now for the level of significance
`\alpha` = 0.05 and the critical value for a right talied test is
`z_c = 1.64`

Now the test statistic is

`z = (\bar x - u_o)/(\sigma/√(n) )\\\\= (88.5-87)/(9/√(80) )`

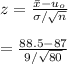
= 1.491

Now it is observed that

Z = 1.49≤z_ c = 1.64

So by this the null hypothesis could not be rejected

So,

P -value = 1 - P(z<1.491)

P-value = 0.068

As p-value = 0.0.68 > 0.05 the null hypothesis could not be rejected