Answer:
The value is
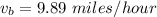
Explanation:
From the question we are told that
The velocity of the wind southward is
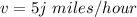
The resultant velocity of the bird with the with wind is
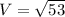
Generally for an object moving in the northwest direction the angle with the horizontal is 45°
Generally the velocity of the bird in the along the x -axis is
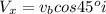
Generally the velocity of the bird in the along the y -axis is
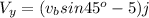
Here
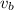 is the velocity of the bird without the wind
is the velocity of the bird without the wind
Generally the resultant velocity of the bird with the with wind is mathematically represented as
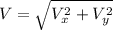
=>
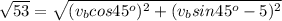
Generally
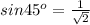
and
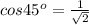
So
![√(53) = \sqrt{(v_b* (\frac{1}{√(2) ))^2 + ([v_b * ((1)/(√(2) ) ]- 5)^2 )]()
=>
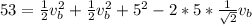
=>
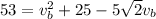
=>
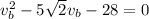
Solving the above quadratic equation using quadratic formula we obtain that
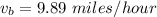
The other value is negative so we do not make use of it because we know that the bird is moving in the positive x and y axis