Answer:
The difference in speed of the dog and cat is 2.65 m/s
Step-by-step explanation:
Given that,
Mass of cat = 0.45 times the mass of dog
K.E of dog = 0.55 times K.E of cat
We need to calculate the velocity of dog
Using given data
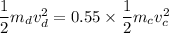

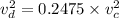
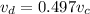 ....(I)
....(I)
The dog speeds up by 0.91 m/s and then has the same kinetic energy as the cat.
We need to calculate the velocity of dog
Using conservation of kinetic energy,
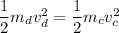
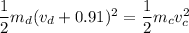
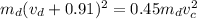
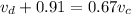
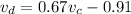 ...(II)
...(II)
From equation (I) and (II)
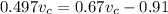
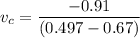
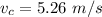
Put the value in equation (I)
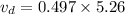
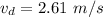
We need to calculate the difference in speed of the dog and cat
Using speed of dog and cat
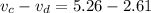

Hence, The difference in speed of the dog and cat is 2.65 m/s