Question

In the past, 49% of those taking a public accounting qualifying exam have passed the exam on their first try. Lately, with the availability of exam preparation books and tutoring sessions may have improved the likelihood of an individual's passing on his or her first try. In a sample of 281 recent applicants, 154 passed on their first attempt. Using the 0.10 level of significance, conduct the analysis to determine whether we can conclude that the proportions passing on their first try has increased. What is the test statistic value from the analysis?

Answer 1

The test statistic Z = 2 < 2.576 at 0.10 level of significance

Null hypothesis is accepted

Explanation:

Step(i):-

Given Population proportion P = 0.49

Q = 1 - P = 1 - 0.49 = 0.51

Given sample proportion

`p^(-) = (x)/(n) = (154)/(281) = 0.548`

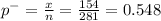
Level of significance = 0.10

Null hypothesis : H₀ : P = 0.49

Alternative Hypothesis :H₁: P≠ 0.49

Step(ii):-

Test statistic

`Z = \frac{p^(-) -P}{\sqrt{(PQ)/(n) } }`

`Z = \frac{0.548-0.49}{\sqrt{(0.49 X 0.51)/(281) } }`

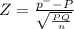
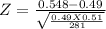
Z = 2

The tabulated value = 2.576

The calculated value Z = 2 < 2.576 at 0.10 level of significance

Null hypothesis is accepted