Answer:
12.03%
Explanation:
The z score i used to measure by how many standard deviations the raw score is above or below the mean. It is given by the equation:
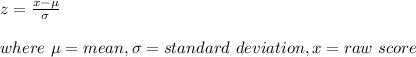
a) For variety A, the mean = μ = 90, standard deviation = σ = 8
For x = 100 grams:
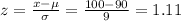
For x = 110 grams:
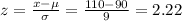
From the normal distribution table, P(100 < X < 110) = P(1.11 < z < 2.22) = P(z < 2.22) - P(z < 1.11) = 0.9868 - 0.8665 = 0.1203 = 12.03%