Question

A swimming pool has the shape of a right circular cylinder with radius 21 feet and height 10 feet. Suppose that the pool is full of water weighing 62.5 pounds per cubic foot. The work W required to pump all the water to the top of the pool is given by W = 4329507.37572 Correct: Your answer is correct. foot-pounds. The work W required to pump all the water to a platform 2 feet above the top of the pool is given by W = foot-pounds.

Answer 1

To find the additional work required to pump water from a right circular cylinder swimming pool to a platform 2 feet above, calculate the weight of the water using the volume of the pool and the given weight per cubic foot, then multiply by the new total height.

Step-by-step explanation:

To calculate the additional work required to pump water to a platform 2 feet above the top of a right circular cylinder swimming pool measuring a radius of 21 feet and a height of 10 feet, we need to adjust the initial work calculation to include the extra height. The weight of the water, which is given as 62.5 pounds per cubic foot, plays a crucial role in determining the work done. We previously calculated the work W to lift the water to the top of the pool to be 4329507.37572 foot-pounds.

When lifting the water an additional 2 feet above the pool, we add this extra distance to the original height the water needs to be raised. This results in a new work calculation:

W = weight of water * (height of the pool + 2 feet)

To find the volume of the pool (V), we use the formula for the volume of a cylinder V = π * radius^2 * height. Since the radius is 21 feet and the height is 10 feet, the volume V can be calculated as V = π * (21 feet)^2 * 10 feet. Then we multiply the volume by the weight of the water per cubic foot to get the total weight.

The additional work W can then be calculated by multiplying the total weight of the water by the new height (height of the pool + additional 2 feet). Finally, this gives us the total work required to pump all the water to the platform that is 2 feet above the pool.

Answer 2

The water required to pump all the water to a platform 2 feet above the top of the pool is is 6061310.32 foot-pound.

Step-by-step explanation:

Given that,

Radius = 21 feet

Height = 10 feet

Weighing = 62.5 pounds/cubic

Work = 4329507.37572

Height = 2 feet

Let's look at a horizontal slice of water at a height of h from bottom of pool

We need to calculate the area of slice

Using formula of area

`A=\pi r^2`

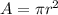
Put the value into the formula

`A=\pi*21^2`

`A=441\pi\ feet^2`

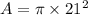
Thickness of slice
`t=\Delta h\ ft`

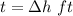
The volume is,

`V=(441\pi*\Delta h)\ ft^3`

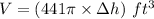
We need to calculate the force

Using formula of force

`F=W* V`

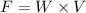
Where, W = water weight

V = volume

Put the value into the formula

`F=62.5*(441\pi*\Delta h)`

`F=27562.5\pi*\Delta h\ lbs`

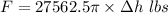
We need to calculate the work done

Using formula of work done

`W=F* d`

Put the value into the formula

`W=27562.5\pi*\Delta h*(10-h)\ ft\ lbs`

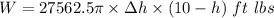
We do this by integrating from h = 0 to h = 10

We need to find the total work,

Using formula of work done

`W=\int_(0)^(h){W}`

Put the value into the formula

`W=\int_(0)^(10){27562.5\pi\\times(10-h)}dh`

`W=27562.5\pi(10h-(h^2)/(2))_(0)^(10)`

`W=27562.5\pi(10*10-(100)/(2)-0)`

`W=4329507.37572`

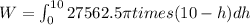
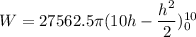
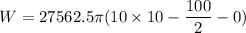
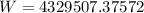
To pump 2 feet above platform, then each slice has to be lifted an extra 2 feet,

So, the total distance to lift slice is (12-h) instead of of 10-h

We need to calculate the water required to pump all the water to a platform 2 feet above the top of the pool

Using formula of work done

`W=\int_(0)^(h){W}`

Put the value into the formula

`W=\int_(0)^(10){27562.5\pi\\times(12-h)}dh`

`W=27562.5\pi(12h-(h^2)/(2))_(0)^(10)`

`W=27562.5\pi(12*10-(100)/(2)-0)`

`W=1929375\pi`

`W=6061310.32\ foot- pound`

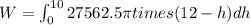
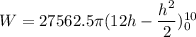
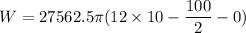
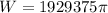
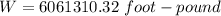
Hence, The water required to pump all the water to a platform 2 feet above the top of the pool is is 6061310.32 foot-pound.