Question

In ​, there were immigrants admitted to a country. In 1960​, the number was . a. Assuming that the change in immigration is​ linear, write an equation expressing the number of​ immigrants, y, in terms of​ t, the number of years after 1900. b. Use your result in part a to predict the number of immigrants admitted to the country in . c. Considering the value of the​ y-intercept in your answer to part a​, discuss the validity of using this equation to model the number of immigrants throughout the entire 20th century. a. A linear equation for the number of immigrants is y nothing.

Answer 1

The answer is below

Explanation:

The complete question is:

In 1960​, there were 237,794 immigrants admitted to a country. In 2001, the number was 1,150,729.

a. Assuming that the change in immigration is​ linear, write an equation expressing the number of​ immigrants, y, in terms of​ t, the number of years after 1900.

b. Use your result in part a to predict the number of immigrants admitted to the country in 2013.

c. Considering the value of the​ y-intercept in your answer to part a​, discuss the validity of using this equation to model the number of immigrants throughout the entire 20th century.

Answer:

a) From the question, we can get two ordered pairs which are
`(t_1,y_1)=(60,237794)\ and\ (t_2,y_2)=(101,1150729)`

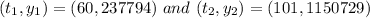
Using the equation of a line given two points:

`y-y_1=(y_2-y_1)/(t_2-t_1)(t-t_1)\\ \\y-237794=(1150729-237794)/(101-60)( t-60)\\\\y-237797=22266.71(t-60)\\\\y=22266.71t-1098205.44`

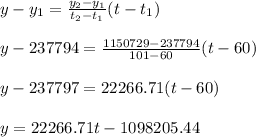
b) In 2013, t = 2013 - 1900 = 113.

Hence:

`y=22266.71t-1098205.44\\\\y=22266.71(113)-1098205.44\\\\y=1417932.488\\\\y=1417933`

c)

`y=22266.71t-1098205.44\\\\the\ y\ intercept\ is\ at\ t=0,hence:\\\\y=22266.71(0)-1098205.44\\\\y=-1098205.44`

Since the y intercept is negative, that is in 1900 the number of immigrants was -1098206 which can not be possible. Hence this equation is not valid and the growth may or may not be linear.