Question

Below is an "oracle" function. An oracle function is a function presented interactively. When you type in a t value, and press the --f--> button the value f(t) appears in the right hand window. There are three lines, so you can calculate three different values of the function at one time. The function f(t) represents the height in feet of a ball thrown into the air, t seconds after it has been thrown. Calculate the instantaneous velocity 1.02 seconds after the ball has been thrown. Instantaneous velocity at 1.02 =

Answer 1

The rate of change of height with respect to time is -10.64 feet/sec

Step-by-step explanation:

Given that,

There are three lines, so you can calculate three different values of the function at one time.

The function f(t) represents the height in feet of a ball thrown into the air, t seconds after it has been thrown.

Given table is,

Time t = 0, 1, 1,02

Function is,
`F(t)=-3.053113177191196*10^(-18),6.000000000000134, 6.41760000000015`

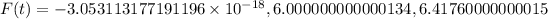
We need to calculate the initial height of ball

Using equation of motion

`h=h_(0)+ut-(1)/(2)gt^2`

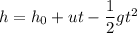
Where, h₀ = initial height

u = initial velocity

t = time

g = acceleration due to gravity

At t = 0,

Put the value into the formula

`-3.053113177191196*10^(-18)=h_(0)+0-0`

`h_(0)=-3.053113177191196*10^(-18)`

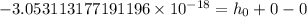
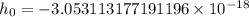
We need to calculate the height of ball at t = 1

Using equation of motion

`h_(1)=h_(0)+u_(0)t-(1)/(2)gt^2`

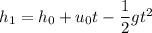
Put the value in the equation

`6.000000000000134=-3.053113177191196*10^(-18)+u-(1)/(2)*32`

`6.000000000000134+3.053113177191196*10^(-18)+16=u_(0)`

`u_(0)=22\ feet/s`

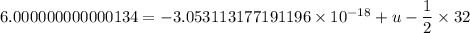
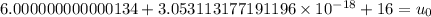
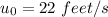
Velocity is the rate of change of height with respect to time

So, velocity at 1.02 sec is given

We need to calculate the height

Using equation of motion

`h=ut-(1)/(2)gt^2`

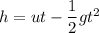
On differentiating w.r.to t

`h'(t)=u-(1)/(2)g(2t)`

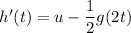
Put the value into the formula

`h'(t)=22-*32*(1.02)`

`h'(t)=-10.64\ feet/sec`

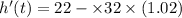
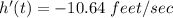
Hence, The rate of change of height with respect to time is -10.64 feet/sec.