Answer:
120°
Explanation:
The external angle <C outside the circle can be expressed in terms of length of arc AE and BD using the formula below.
<C =
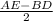
Next is to make the length of arc AE the subject of the formula;
<C =
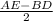
cross multiply
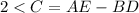
add BD to both sides of the equation
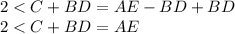
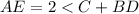
Given
<C = 36°
arc BD = 48°
Substitute the given parameters into the formula;
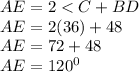
Hence mArc is 120°