Answer:
The parametrization of the curve on the surface is
![c(t) = [x(t) , y(t), z(t)] \equiv [(√(97) )/(2) cost - 4 , (√(97) )/(2) sint + (5)/(2) , 5(√(97) )/(2) sint -8 (√(97) )/(2) cost +(93)/(2) ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1y2fusttt8bvd5gbzu1e652ifkx8kr0b63.png)
Where
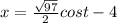
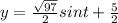
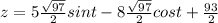
Explanation:
From the question we are told that
The equation for the paraboloid is

The equation of the plane is
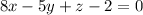
Form the equation of the plane we have that
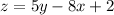
So

=>
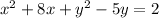
Using completing the square method to evaluate the quadratic equation we have
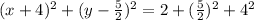
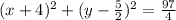

representing the above equation in parametric form
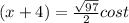 ,
,
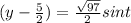
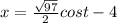
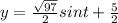
So from
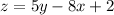
![z = 5[(√(97) )/(2) sint + (5)/(2)] -8[ (√(97) )/(2) cost - 4] +2](https://img.qammunity.org/2021/formulas/mathematics/high-school/eeaqwsh41i0tv0v5i5y3iiksdfhh1gij86.png)
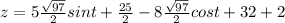
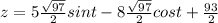
Generally the parametrization of the curve on the surface is mathematically represented as
![c(t) = [x(t) , y(t), z(t)] \equiv [(√(97) )/(2) cost - 4 , (√(97) )/(2) sint + (5)/(2) , 5(√(97) )/(2) sint -8 (√(97) )/(2) cost +(93)/(2) ]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1y2fusttt8bvd5gbzu1e652ifkx8kr0b63.png)