Answer:
The distance between the two cars is approximately 237 meters.
Explanation:
Let be P the top of the high-rise building and Q and R the location of the two cars from each side of the tower. Geometric figure is represented on image attached below. We calculate the distance between both cars (
 ), measured in meters, by Trigonometric ratios:
), measured in meters, by Trigonometric ratios:
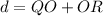
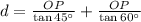
Where
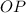 is the height of the building, measured in meters.
is the height of the building, measured in meters.
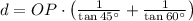
If we know that
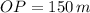 , then:
, then:
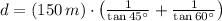
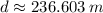
The distance between the two cars is approximately 237 meters.