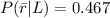Answer:
a
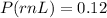
b
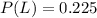
c
Explanation:
The chance that it will rain is
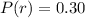
The chance that it does not rain is

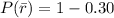
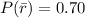
The probability that the bus run late if it rains is
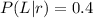
The probability that the bus run late if it does not rain is
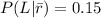
Generally the probability that it will rain and the bus will be late is mathematically represented as
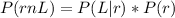
=>

=>
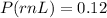
Generally the probability that the bus will be late is mathematically represented as
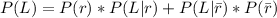
=>
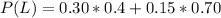
=>
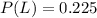
Generally given that the bus ran late, the probability that the bus it was not raining is mathematically represented as
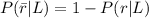
Here
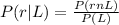
=>
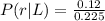
=>

So

=>