Question

Instruments in an airplane which is in level flight indicate that the velocity relative to the air (airspeed) is 180.00 km/h and the direction of the relative velocity vector (heading) is 70° east of north. Instruments on the ground indicate that the velocity of the airplane (ground speed) is 150.00 km/h and the direction of flight (course) is 60° east of north. Determine the wind speed and direction. (Round the final answer to two decimal places.)

Answer 1

Step-by-step explanation:

From the given information:

The coordinate axis is situated in the east and north direction.

So, the north will be the y-axis and the east will be the x-axis

Similarly, the velocity of the plane in regard to the air in the coordinate system will be
`v_(P/A) = v( cos \theta \ i + sin \theta \ j)`

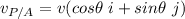
where:

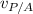`v_(P/A)` = velocity of the plane in regard to the air

v = velocity

θ = angle of inclination of the plane with respect to the horizontal

replacing v = 180 km/ and θ = 20° in above equation, then:

The velocity of the airplane in the coordinate system as:

`v_(P) = v_o( cos \phi \ i + sin \phi \ j)`

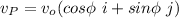
where;

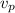`v_p` = velocity of the airplane

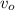`v_o` = velocity

∅ = angle of inclination with regard to the base axis;

Then; replacing
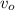`v_o` = 150 km/h and ∅ = 30°

Therefore, the velocity of the plane in the system is :

`v_p = v_A + v_(P/A)`

`v_A= v_P -v_(P/A)` --- (1)

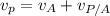
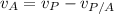`v_A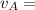=` ( 150 cos 30° - 180 cos 20°)i + ( 150 sin 30° - 180sin 20°)j

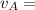`v_A=` (-39.24 km/h)i + (13.44 km/h) j

The magnitude is:

`v_A= (-39.24 km/h)i + (13.44 km/h) j`

`|v_A|^2 = √( (-39.24 km/h)^2+ (13.44 km/h)^2)`

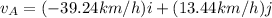
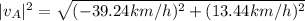
`v_A` = 41.48 km/h

The airplane is moving at an angle of the inverse tangent to the abscissa and ordinate.

The angle of motion is:

tan θ = 39.24/13.44

tan θ = 2.9

θ =
`tan ^(-1) (2.9)`

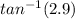
θ = 70.97°

The angle of motion is 70.97° from west of north with a velocity of 41.48 km/h.