Answer:
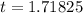
Explanation:
Given
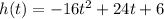
Required
When will the coin hit the ground
When the coin hits the ground,

The expression
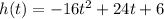 becomes
becomes
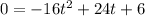
Multiply through by -1
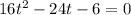
Solve using quadratic formula

Where
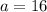
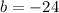
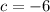

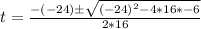

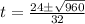
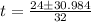
Split
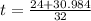 or
or
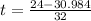
 or
or
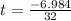
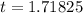 or
or
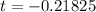
But time can't be negative;
So:
Time to hit the ground is 1.71825 seconds