Question

What is the direction of a vector with an x component of -12 m and a y component of 21 m?

Answer 1

`Direction= 119.74^\circ`

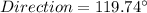
Step-by-step explanation:

Displacement Vector

The displacement, as every vector, has a magnitude r and a direction angle θ measured from the positive x-axis.

If we know the x-y components of the displacement, the magnitude and angle can be calculated by the equations:

`r=√(x^2+y^2)`

`\displaystyle \tan\theta=(y)/(x)`

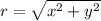
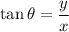
The coordinates of the given vector are x=-12 m, y=21 m, thus:

`\displaystyle \tan\theta=(21)/(-12)=-1.75`

`\theta=tan^(-1)(-1.75)=-60.26^\circ`

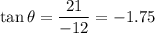
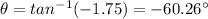
Since the vector lies in the second quadrant, we add 180° to find the correct direction:

`\boxed{Direction=-60.26^\circ+180^\circ= 119.74^\circ}`