Question

A body moving in the positive x direction passes the origin at time t=0 . Between t=0 and t=1 second , the body has a constant speed of 24 metres per second . At t=1 second , the body is given a constant acceleration of 6 metres per second squared in the negative x direction . The position at t=11 seconds is?

Answer 1

The position at t=11 seconds is -96 m or 96 m to the left of the origin

Step-by-step explanation:

Constant speed and constant acceleration motion

If a body travels the same distance per unit of time, the body has a constant speed. The equation for the distance x is:

`x=v.t`

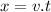
Where v is the constant speed and t is the time.

At time t=0 the body is moving at a constant speed of v=24 m/s in the positive x-direction. It keeps that condition for t=1 sec. The distance traveled is:

`x=24m/s\cdot 1\ s=24\ m`

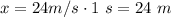
Now the body is given a constant acceleration of 6 m/s^2 in the negative x-direction, that is, a=-6 m/s^2

The distance traveled by a body at constant acceleration is given by:

`\displaystyle x=v_o.t+(a.t^2)/(2)`

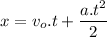
Where vo is the initial speed and t is the time.

We need to find the position at t=11 sec, but we must subtract the one second already passed, thus t=10 s

`\displaystyle x=24m/s\cdot 10s+(-6m/s^2.(10)^2)/(2)`

`\displaystyle x=240\ m-360\ m=-120\ m`

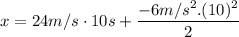
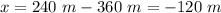
This distance must be added to the actual position of the body, that is:

-120 m + 24 m = -96 m

The position at t=11 seconds is -96 m or 96 m to the left of the origin