Answer:
Approximately
 and approximately
and approximately
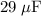 .
.
Step-by-step explanation:
Let
 and
and
 denote the capacitance of these two capacitors.
denote the capacitance of these two capacitors.
When these two capacitors are connected in parallel, the combined capacitance will be the sum of
 and
and
 . (Think about how connecting these two capacitors in parallel is like adding to the total area of the capacitor plates. That would allow a greater amount of charge to be stored.)
. (Think about how connecting these two capacitors in parallel is like adding to the total area of the capacitor plates. That would allow a greater amount of charge to be stored.)
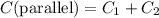 .
.
On the other hand, when these two capacitors are connected in series, the combined capacitance should satisfy:
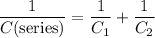 .
.
(Consider how connecting these two capacitors in series is similar to increasing the distance between the capacitor plates. The strength of the electric field (
 ) between these plates will become smaller. That translates to a smaller capacitance if the amount of charge stored
) between these plates will become smaller. That translates to a smaller capacitance if the amount of charge stored
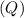 stays the same.)
stays the same.)
The question states that:
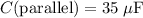 , and
, and
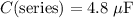 .
.
Let the capacitance of these two capacitors be
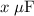 and
and
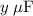 . The two equations will become:
. The two equations will become:
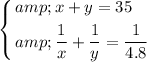 .
.
From the first equation:
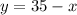 .
.
Hence, the
 in the second equation here can be replaced with
in the second equation here can be replaced with
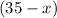 . That equation would then become:
. That equation would then become:
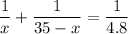 .
.
Solve for
 :
:
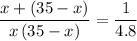 .
.
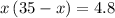 .
.
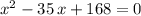 .
.
Solve this quadratic equation for
 :
:
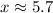 or
or
 .
.
Substitute back into the equation
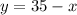 for
for
 :
:
In other words, these two capacitors have only one possible set of capacitances (even though the previous quadratic equation gave two distinct real roots.) The capacitances of the two capacitors would be approximately
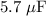 and approximately
and approximately
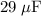 (both values are rounded to two significant digits.)
(both values are rounded to two significant digits.)