Question

PLEASE HELP!!!!! DUE TODAY!!!!!

A customer orders two ice cream cones. How much ice cream will you need to use to fill the two ice cream cones to the top? Show the mathematics you used to solve. Use units to express your answer.

Answer 1

12.4 cm³

Explanation:

From the picture attached,

Radius of the circular top of the cone =
`\frac{\text{Diameter}}{2}` =
`(2)/(2)=1`

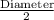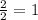
Height of the cone = h

Lateral height of the cone = h

By applying Pythagoras theorem in the right triangle of the cone,

l² = r² + h²

6² = 1² + h²

h =
`√(36-1)`

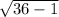
h =
`√(35)`

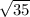
Ice cream needed to fill one cone = Volume of the cone

Since, formula for the volume of the cone V =
`(1)/(3) \pi r^(2) h`

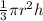
V =
`(1)/(3)\pi (1)^2(√(35))`

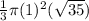
= 6.195

≈ 6.20 cm³

Ice cream needed to fill the two cones = 2 × 6.20

= 12.4 cm³

Therefore, ice cream needed to fill the two cone = 12.4 cm³