Question

Write an equation in slope-intercept form of the line that bisects the angle formed by BA and BC

Answer 1

Given:

Angled formed by ray BA and ray BC is 90 degrees.

To find:

The equation of line that bisects the angle formed by ray BA and ray BC.

Solution:

If a line bisects the angle formed by ray BA and ray BC, then it must be passes through point B and makes angles of 45 degrees with ray BA and ray BC.

It is possible if the line passes though point B(-1,3) and other point (-2,4).

Equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`y-3=(4-3)/(-2-(-1))(x-(-1))`

`y-3=(1)/(-1)(x+1)`

`y-3=-x-1`

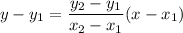
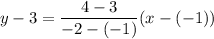
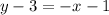
Add 3 on both sides.

`y=-x-1+3`

`y=-x+2`

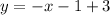
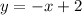
Therefore, the required equation of line is
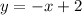`y=-x+2`.