Answer:
The domain of the function b(s) is
![s\in[0,150]](https://img.qammunity.org/2021/formulas/mathematics/college/40egdq3x0pb7q8u49s9ruh189dc6yebyzy.png)
Explanation:
Given that, a total of 560 books is added to the book shelf each morning.
 be the number of the students who visit the library on a particular day and takes exactly 3 books from this shelf.
be the number of the students who visit the library on a particular day and takes exactly 3 books from this shelf.
So, the number of books they take from the shelf is 3s.
The number of remaining books the shelf
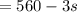 .
.
As , given that
 be the number of books left on the shelf at the end of that day, so the required function,
be the number of books left on the shelf at the end of that day, so the required function,
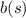 , is
, is
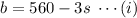
As there are 150 students in the school. So, if no one will go to the library, than
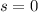 which is the minimum value, and if all goes to the library , than
which is the minimum value, and if all goes to the library , than
 which is the maximum value of
which is the maximum value of
 .
.
So, the possible value of s is:
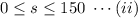
Now, as there is no book left or there are some books left the negative value of
 is not possible. So,
is not possible. So,
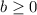
 [fron equation (i)]
[fron equation (i)]
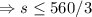
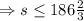
as s id the number of students which cant be a fractional value, so the possible nearest value is,

From the equations (ii) and (iii), the domain of the function
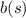 is
is
![s\in[0,150]](https://img.qammunity.org/2021/formulas/mathematics/college/40egdq3x0pb7q8u49s9ruh189dc6yebyzy.png)