Answer:
C
Explanation:
We know that the volume of a cylinder is given by the formula:
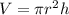
And we want to find the expression that represents the volume when the radius is (x+8) and the height is (2x+3).
So, let's substitute (x+8) for r and (2x+3) for h. This yields:
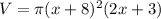
Let's expand.
Expand the square term first. We can use the perfect square trinomial pattern, which is:
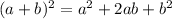
Here, our a is x and b is 8. So:
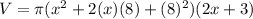
Simplify:
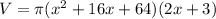
Expand further. This time, we will use the distribute property. So:
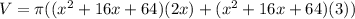
Multiply:
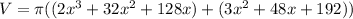
Combine like terms:
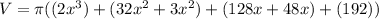
Add:
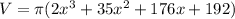
Distribute the π:
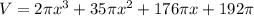
So, our answer is C.
And we're done!