Given:
Given that the radius of the circle is 2 inches.
We need to determine the area of the remaining square.
Area of a square:
Given that each circle has a radius of 2 inches.
Then, the diameter of each circle is 4 inches.
Hence, the side length of the square is 2 × 4 = 8 inches.
The area of the square is given by
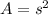
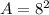
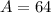
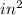
Thus, the area of the square is 64 square inches.
Area of the four circles:
The area of one circle is given by

Substituting r = 2, we have;
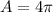
Thus, the area of one circle is 4π in²
The area of 4 circles is 4 × 4π =16π in²
Hence, the area of the 4 circles is 16π in²
Area of the remaining square:
The area of the remaining square is given by
Area = Area of the square - Area of four circles.
Substituting the values, we get;
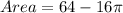
Thus, the area of the remaining square is (64 - 16π) in²
Hence, Option c is the correct answer.