Question

A company makes a profit of $60 per software program and $45 per video game. The company must produce both and can produce at most 225 software programs and at most 350 video games per week. Total production cannot exceed 455 items per week.

(a) Write out the set of inequalities you would use to represent the constraints in this situation.
(b) Identify the corner points.
(c) How many items of each kind should be produced per week to maximize profit? Show your work. Be sure
to show the comparison in your work.
Use linear programming to solve.

Answer 1

Explanation:

a)

(a)255+350 <455

ans...605-455

..150

.........profit per week is 60 +45

105.

105 x 150

weekly profit is..$15750

Answer 2

See below.

Explanation:

Let's first define our variables. Let's let:

x denote the amount of software programs made and

y denote the amount of video games made.

Part A)

Now, let's write our equations and constraints.

The company can produce at most 225 software programs. So:

`x\leq225`

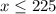
And the company can produce at most 350 video games. So:

`y\leq 350`

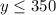
Total product (the sum of software programs and video games) cannot exceed 455 items per week. In other words:

`x+y\leq455`

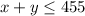
Part B)

Refer to the first graph:

We have four corner points: A, B, C, and D.

The darkest portion represents the feasible portion. Any combination of software programs and video games within this portion can be produced.

Part C)

Refer to the second graph.

To find what to produce to find the maximum profit, let's write an equation. Let P equal to maximum profit. So, it would be the sum of the total profit from the software programs and video games. We can write the following equation:

`P=60x+45y`

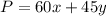
Let's solve for y in order to graph it. Subtract 60x from both sides:

`45y=-60x+P`

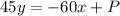
Divide both sides by 45:

`y=-(4)/(3)x+(P)/(45)`

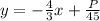
In order produce the maximum profit, P must be the greatest while simultaneously touching our corner points.

Note: The P, Q, R, and S are just rough estimates.

I've graphed four versions of our equation using different variables (for P). We can see that the equation with the highest profit P is the one the crosses point C with P equaling approximately $24,000.

Therefore, in order to maximize profits, the company should produce (Remember that C is at (225, 230)) 225 software programs and 230 video games.

And we're done!