Final answer:
The equation has one solution. Upon solving
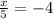 , we find that x equals -20, which can be verified by substituting back into the original equation.
, we find that x equals -20, which can be verified by substituting back into the original equation.
Step-by-step explanation:
The student asks to evaluate whether the equation
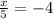 has one solution, no solutions, or an infinite number of solutions. This equation has exactly one solution because it's a linear equation with one variable. To find the solution, we multiply both sides of the equation by 5 to isolate x:
has one solution, no solutions, or an infinite number of solutions. This equation has exactly one solution because it's a linear equation with one variable. To find the solution, we multiply both sides of the equation by 5 to isolate x:
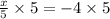
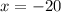
Thus, the value of x that satisfies the equation is -20. Since the equation is linear and straightforward, there is no additional value for x; hence, -20 is the only solution that makes sense. The technique of trying different signs in the numerator applies to specific algebraic problems where a variable can be positive or negative, but it does not apply to this simple linear equation. To confirm that -20 is the right solution, you can substitute it back into the original equation:
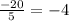
This verifies that -20 divided by 5 is indeed -4, confirming the solution is correct.