Answer:
The numerical length of RS is 22 units
Explanation:
∵ Point S is on the line segment RT
→ That means S divide RT into two parts RS and ST
∴ RS + ST = RT
∵ RS = 4x - 10
∵ ST = 2x - 10
∵ RT = 4x - 4
→ Substitute them in the statement above
∴ 4x - 10 + 2x - 10 = 4x - 4
→ Add the like terms in the left side
∴ (4x + 2x) + (-10 + -10) = 4x - 4
∴ 6x + (-20) = 4x - 4
∴ 6x - 20 = 4x - 4
→ Add 20 to both sides
∴ 6x -20 + 20 = 4x - 4 + 20
∴ 6x = 4x + 16
→ Subtract 4x from both sides
∴ 6x - 4x = 4x - 4x + 16
∴ 2x = 16
→ Divide both sides by 2 to find x
∴
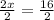
∴ x = 8
→ Substitute the value of x in Rs to find its length
∵ RS = 4(8) - 10
∴ RS = 32 - 10
∴ RS = 22 units
The numerical length of RS is 22 units