Answer:
11)
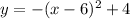
12)

Explanation:
Vertex form of a parabola:
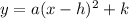 where (h, k) is the vertex
where (h, k) is the vertex
Question 11
From inspection of the graph, the vertex is (6, 4)
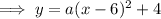
To find
 , substitute the coordinates of a point on the curve into the equation.
, substitute the coordinates of a point on the curve into the equation.
Using point (4, 0):
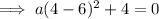
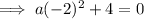
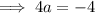
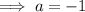
Therefore, the equation of the parabola in vertex form is:
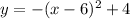
Question 12
From inspection of the graph, the vertex is (-5, 0)
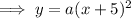
To find
 , substitute the coordinates of a point on the curve into the equation.
, substitute the coordinates of a point on the curve into the equation.
Using point (-3, 4):

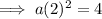

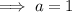
Therefore, the equation of the parabola in vertex form is:
