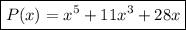Question

Write a polynomial of degree 5 with zero x=0,i square root 7, -2i

Answer 1

`P(x)=x^5+11x^3+28x`

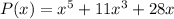
Explanation:

Roots of a polynomial

If we know the roots of a polynomial, say x1,x2,x3,...,xn, we can construct the polynomial using the formula

`P(x)=a(x-x_1)(x-x_2)(x-x_3)...(x-x_n)`

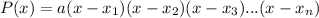
Where a is an arbitrary constant.

We know three of the roots of the degree-5 polynomial are:

`x_1=0;\ x_2=√(7)\boldsymbol{i}:\ x_3=-2\boldsymbol{i}`

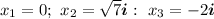
We can complete the two remaining roots by knowing the complex roots in a polynomial with real coefficients, always come paired with their conjugates. This means that the fourth and fifth roots are:

`x_4=-√(7)\boldsymbol{i}:\ x_3=+2\boldsymbol{i}`

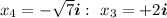
Let's build up the polynomial, assuming a=1:

`P(x)=(x-0)(x-√(7)\boldsymbol{i})(x+√(7)\boldsymbol{i})(x-2\boldsymbol{i})(x+2\boldsymbol{i})`

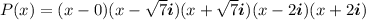
Since:

`(a+b\boldsymbol{i})\cdot (a-b\boldsymbol{i})=a^2+b^2`

`P(x)=(x)(x^2+7)(x^2+4)`

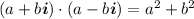
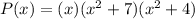
Operating the last two factors:

`P(x)=(x)(x^4+11x^2+28)`

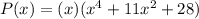
Operating, we have the required polynomial:

`\boxed{P(x)=x^5+11x^3+28x}`